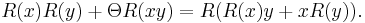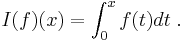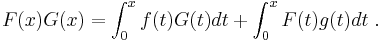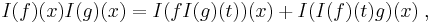Rota–Baxter algebra

In mathematics, a Rota–Baxter algebra is an algebra, usually over a field k, together with a particular k-linear map R which satisfies the weight-θ Rota–Baxter identity. It appeared first in the work of the American mathematician Glen Baxter[1] in the realm of probability theory. Baxter's work was further explored from different angles by Gian-Carlo Rota,[2][3][4] Pierre Cartier,[5] and Frederic V. Atkinson,[6] among others. Baxter’s derivation of this identity that later bore his name emanated from some of the fundamental results of the famous probabilist Frank Spitzer in random walk theory.[7][8]

Contents

Definition and first properties

Let A be a k-algebra with a k-linear map R on A and let θ be a fixed parameter in k. We call A a Rota-Baxter k-algebra and R a Rota-Baxter operator of weight θ if the operator R satisfies the following Rota–Baxter relation of weight θ:

R(x)R(y) %2B \Theta R(xy) = R(R(x)y %2B xR(y)).\,

The operator R:= θ id − R also satisfies the Rota–Baxter relation of weight θ.

Examples

Integration by Parts

Integration by parts is an example of a Rota–Baxter algebra of weight 0. Let 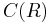C(R) be the algebra of continuous functions from the real line to the real line. Let :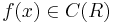f(x) \in C(R) be a continuous function. Define integration as the Rota–Baxter operator

I(f)(x) = \int_0^x f(t) dt \;.

Let G(x) = I(g)(x) and F(x) = I(f)(x). Then the formula for integration for parts can be written in terms of these variables as

F(x)G(x) = \int_0^x f(t) G(t) dt %2B \int_0^x F(t)g(t) dt \;.

In other words

I(f)(x)I(g)(x) = I(fI(g)(t))(x) %2B I(I(f)(t)g)(x) \; ,

which shows that I is a Rota–Baxter algebra of weight 0.

Spitzer identity

The Spitzer identity appeared is named after the American mathematician Frank Spitzer. It is regarded as a remarkable stepping stone in the theory of sums of independent random variables in fluctuation theory of probability. It can naturally be understood in terms of Rota–Baxter operators.

Bohnenblust–Spitzer identity

See also

Notes

  1. ^ Baxter, G. (1960). "An analytic problem whose solution follows from a simple algebraic identity". Pacific J. Math. 10: 731–742. 
  2. ^ Rota, G.-C. (1969). "Baxter algebras and combinatorial identities, I, II.". Bull. Amer. Math. Soc. 75: 325–329. ; ibid. 75, 330–334, (1969). Reprinted in: Gian-Carlo Rota on Combinatorics: Introductory papers and commentaries, J.P.S. Kung Ed., Contemp. Mathematicians, Birkhäuser Boston, Boston, MA, 1995.
  3. ^ G.-C. Rota, Baxter operators, an introduction, In: Gian-Carlo Rota on Combinatorics, Introductory papers and commentaries, J.P.S. Kung Ed., Contemp. Mathematicians, Birkhäuser Boston, Boston, MA, 1995.
  4. ^ G.-C. Rota and D. Smith, Fluctuation theory and Baxter algebras, Instituto Nazionale di Alta Matematica, IX, 179–201, (1972). Reprinted in: Gian-Carlo Rota on Combinatorics: Introductory papers and commentaries, J.P.S. Kung Ed., Contemp. Mathematicians, Birkhäuser Boston, Boston, MA, 1995.
  5. ^ Cartier, P. (1972). "On the structure of free Baxter algebras". Advances in Math. 9: 253–265. 
  6. ^ Atkinson, F. V. (1963). "Some aspects of Baxter’s functional equation". J. Math. Anal. Appl. 7: 1–30. 
  7. ^ Spitzer, F. (1956). "A combinatorial lemma and its application to probability theory". Trans. Amer. Math. Soc. 82: 323–339. 
  8. ^ Spitzer, F. (1976). Principles of random walks. Graduate Texts in Mathematics. 34 (Second ed.). New York, Heidelberg: Springer-Verlag. 

External links